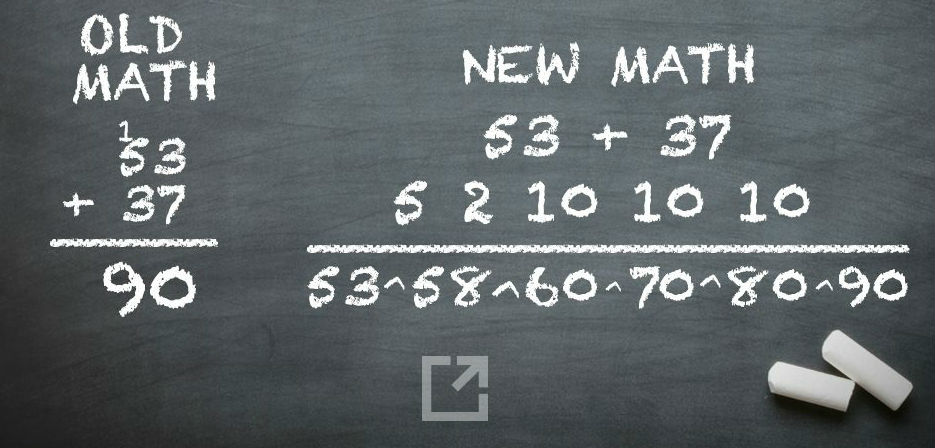If you use Facebook, I’d almost guarantee you’ve seen pictures like this that attack the “new way” teachers are trying to teach students to do Math. I’ve seen posts (or memes) that reference engineers and rocket scientists that cannot figure out why students are using diagrams, charts, and other strategies instead of just doing it the “old way.” I stopped teaching Math before Indiana adopted Common Core, then we unadopted Common Core, and then we modeled our standards on the Common Core. I don’t know how to use the strategies the students use these days, but I don’t miss the old way. I am very impressed and proud that our young people can show so much better Math thinking than I got back in the Stone Age.
The mistake in the thinking of each of these examples is they don’t acknowledge that “old way” is actually a shortcut. I am worse at Math because I was taught the shortcut before I worked through the logic behind it. Take this example:
Many of us know to add 5 and 5, get 10, put the zero at the bottom, and put the 1 above the 1 in 15. It is a shockingly simple way to get an answer, but really no more valuable that using a calculator or asking Siri. I once had a teacher tell me that we learn to do computation because we may be cashiers at some point in the future, and we’ll need to be able to make change if the power goes out. That’s not a very good reason – if the power is out, my credit card machine is probably down too! So instead of learning computation for its own sake, we should gain all the logic and “number sense” we can from arithmetic to make our students best prepared for Algebra, Geometry, and even higher Math. Back to our example from above; the new approach asks us to recognize 15+5 is working with groups of 5, or it shows us that we combine individual units into groups of 10, etc.
Another problem with the criticism of the new Math is that it doesn’t agree with the criticism we receive from employers that potential employees aren’t problem solvers. I doubt those employers are saying “These applicants can’t do 3 digit subtraction on paper!” I imagine that in most jobs someone is faced with a problem, not unlike a word problem, and the worker needs to strategize how to get to the solution. Those problems are also more likely to involve algebra, or at least order of operations. These approaches that ask students to break up numbers into components and put them together in different ways – those mimic the algebra they’ll be doing in a few short years. Here is where I wanted to explain how the box method elementary students use for multiplication is directly applicable to binomials, but this website does a much better job explaining it than I would: https://medium.com/i-math/how-common-core-can-prepare-students-518c2fb72e3
In college I was taught to do arithmetic in base 6 to get “under the hood” on why our computation shortcuts work. I am the principal, and I don’t understand all the techniques our teachers are teaching the students. I saw problems on 1st and 2nd grade assessments that challenged me, but isn’t that really cool? I’m not at the pinnacle where students work hard to approach my great knowledge; I’m an old guy that reached a level, and our students will far surpass any level I’ve reached. We are preparing them for jobs that don’t even exist yet. If you are tempted to throw out our Math book because your child’s homework doesn’t make sense to you, just smile and do the same thing I do with my kid – tell him or her:
“I didn’t learn it that way. Your teacher is teaching you a really interesting way, but I cannot help you. I’ll write a note here that says we couldn’t figure it out at home, and your teacher will help you with it in class. Once you understand it, come and show me because I’m really interested in what you’re learning!